Gerak Lurus Berubah Beraturan (GLBB)
A. Konsepsi Gerak Lurus Berubah Beraturan (GLBB)

 Selama bola bergerak vertikal ke atas, gerakan bola melawan gaya gravitasi yang menariknya ke bumi. Akhirnya bola bergerak diperlambat. Akhirnya setelah mencapai ketinggian tertentu yang disebut tinggi maksimum (h max), bola tak dapat naik lagi. Pada saat ini kecepatan bola nol (Vt = 0). Oleh karena tarikan gaya gravitasi bumi tak pernah berhenti bekerja pada bola, menyebabkan bola bergerak turun. Pada saat ini bola mengalami jatuh bebas....
Selama bola bergerak vertikal ke atas, gerakan bola melawan gaya gravitasi yang menariknya ke bumi. Akhirnya bola bergerak diperlambat. Akhirnya setelah mencapai ketinggian tertentu yang disebut tinggi maksimum (h max), bola tak dapat naik lagi. Pada saat ini kecepatan bola nol (Vt = 0). Oleh karena tarikan gaya gravitasi bumi tak pernah berhenti bekerja pada bola, menyebabkan bola bergerak turun. Pada saat ini bola mengalami jatuh bebas....
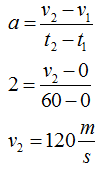
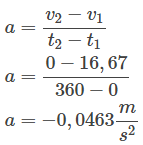
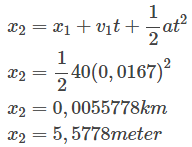

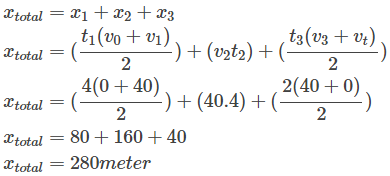
Gerak lurus berubah beraturan (GLBB) adalah gerak benda dalam lintasan garis lurus dengan percepatan tetap. Jadi, ciri utama GLBB adalah bahwa dari waktu ke waktu kecepatan benda berubah, semakin lama semakin cepat/lambat...sehingga gerakan benda dari waktu ke waktu mengalami percepatan/perlambatan. Dalam artikel ini, kita tidak menggunakan istilah perlambatan untuk gerak benda diperlambat. Kita tetap saja menamakannya percepatan, hanya saja nilainya negatif. Jadi perlambatan sama dengan percepatan negatif.
Contoh sehari-hari GLBB adalah peristiwa jatuh bebas. Benda jatuh dari ketinggian tertentu di atas permukaan tanah. Semakin lama benda bergerak semakin cepat. Kini, perhatikanlah gambar di bawah yang menyatakan hubungan antara kecepatan (v) dan waktu (t) sebuah benda yang bergerak lurus berubah beraturan dipercepat.
vt = kecepatan akhir (m/s)
a = percepatan
t = selang waktu (s)
Perhatikan bahwa selama selang waktu t , kecepatan benda berubah dari vo menjadi vt sehingga kecepatan rata-rata benda dapat dituliskan:
S = jarak yang ditempuh
seperti halnya dalam GLB (gerak lurus beraturan) besarnya jaraktempuh juga dapat dihitung dengan mencari luasnya daerah dibawah grafik v - t
Bila dua persamaan GLBB di atas kita gabungkan, maka kita akan dapatkan persamaan GLBB yang ketiga.....
B. Contoh-Contoh GLBB
1. Gerak Jatuh Bebas
Ciri khasnya adalah benda jatuh tanpa kecepatan awal (vo = nol). Semakin ke bawah gerak benda semakin cepat.Percepatan yang dialami oleh setiap benda jatuh bebas selalu sama, yakni sama dengan percepatan gravitasi bumi (a = g) (besar g = 9,8 m/s2 dan sering dibulatkan menjadi 10 m/s2)
Rumus gerak jatuh bebas ini merupakan pengembangan dari ketiga rumus utama dalam GLBB seperti yang telah diterangkan di atas dengan modifikasi : s (jarak) menjadi h (ketinggian) dan vo = 0 serta percepatan (a) menjadi percepatan grafitasi (g).
coba kalian perhatikan rumus yang kedua....dari ketinggian benda dari atas tanah (h) dapat digunakan untuk mencari waktu yang diperlukan benda untuk mencapai permukaan tahah atau mencapai ketinggian tertentu... namun ingat jarak dihitung dari titik asal benda jatuh bukan diukur dari permukaan tanah
sebagai contoh : Balok jatuh dari ketinggian 120 m berapakah waktu saat benda berada 40 m dari permukaan tanah?
jawab : h = 120 - 40 = 80 m

t = 4 s
2. Gerak Vertikal ke Atas
 Selama bola bergerak vertikal ke atas, gerakan bola melawan gaya gravitasi yang menariknya ke bumi. Akhirnya bola bergerak diperlambat. Akhirnya setelah mencapai ketinggian tertentu yang disebut tinggi maksimum (h max), bola tak dapat naik lagi. Pada saat ini kecepatan bola nol (Vt = 0). Oleh karena tarikan gaya gravitasi bumi tak pernah berhenti bekerja pada bola, menyebabkan bola bergerak turun. Pada saat ini bola mengalami jatuh bebas....
Selama bola bergerak vertikal ke atas, gerakan bola melawan gaya gravitasi yang menariknya ke bumi. Akhirnya bola bergerak diperlambat. Akhirnya setelah mencapai ketinggian tertentu yang disebut tinggi maksimum (h max), bola tak dapat naik lagi. Pada saat ini kecepatan bola nol (Vt = 0). Oleh karena tarikan gaya gravitasi bumi tak pernah berhenti bekerja pada bola, menyebabkan bola bergerak turun. Pada saat ini bola mengalami jatuh bebas....
Jadi bola mengalami dua fase gerakan. Saat bergerak ke atas bola bergerak GLBB diperlambat (a = - g) dengan kecepatan awal tertentu lalu setelah mencapai tinggi maksimum bola jatuh bebas yang merupakan GLBB dipercepat dengan kecepatan awal nol.
Pada saat benda bergerak naik berlaku persamaan :
vo = kecepatan awal (m/s)
g = percepatan gravitasi
t = waktu (s)
vt = kecepatan akhir (m/s)
h = ketinggian (m)
3. Gerak Vertikal ke Bawah
Berbeda dengan jatuh bebas, gerak vertikal ke bawah yang dimaksudkan adalah gerak benda-benda yang dilemparkan vertikal ke bawah dengan kecepatan awal tertentu. Jadi seperti gerak vertikal ke atas hanya saja arahnya ke bawah. Sehingga persamaan-persamaannya sama dengan persamaan-persamaan pada gerak vertikal ke atas, kecuali tanda negatif pada persamaan-persamaan gerak vertikal ke atas diganti dengan tanda positif.
C. Rangkuman GLB dan GLBB
D. Contoh Soal dan jawaban Gerak Lurus Berubah Beraturan
Sebelumnya kita membahas tentang gerak lurus berubah beraturan atau GLBB yaitu tentang pengertiannya serta persamaan atau rumus-rumusnya, maka sekarang giliran contoh soal dan jawabannya.
Contoh soal pertama
Sebuah mobil yang berhenti di tempat parkir tiba-tiba bergerak dengan percepatan 2 meter/sekon2. Berapa kecepatan mobil tersebut setelah selang waktu 1 menit?.
Jawab
Mobil mula-mula berhenti pada saat t1 = 0 s, maka v1 = 0 m/s. Dengan menggunakan perhitungan berikut ini kita bisa mengetahui kecepatan mobil pada saat 1 menit = 60 s.
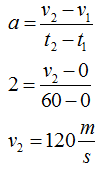
Jadi kecepatan mobl tersebut saat t = 1 menit yaitu 120 m/s.
Contoh soal kedua
Ada sebuah truk mula-mula bergerak dengan kecepatan 60 km/jam. Berapa besar percepatan truk tersebut agar truk dapat berhenti pada waktu 6 menit?
Jawab
Diketahui:
v1 = 60 km/jam = 60.000 : 3600 = 16,67 m/s
v2= 0 km/jam = 0 m/s
t1= o s
t2= 6 menit = 360 s
a = ….?
v1 = 60 km/jam = 60.000 : 3600 = 16,67 m/s
v2= 0 km/jam = 0 m/s
t1= o s
t2= 6 menit = 360 s
a = ….?
Dengan menggunakan persamaan seperti pada contoh satu, kita dapat mengetahui percepatannya yaitu
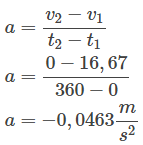
Nilai minus (-) merupakan tanda bahwa truk tersebut mengalami perlambatan.
Contoh soal ketiga
Sebuah mobil berhenti di pinggir jalan. Kemudian bergerak dengan percepatan 40 km/jam2. Berapa jarak yang dapat ditempuh mobil tersebut dalam 1 menit?
Jawab
Diketahui:
a = 40 km/jam2
t = 1 menit = 0,0167 jam
x1= 0
v1= 0
x2= …..?
a = 40 km/jam2
t = 1 menit = 0,0167 jam
x1= 0
v1= 0
x2= …..?
Dengan menggunakan persamaan (3) kita bisa melakukan perhitungan menjadi seperti ini
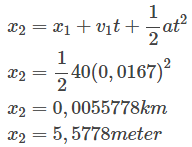
Jadi dalam waktu 1 menit mobil terebut akan menempuh jarak sebesar 5,5578 meter dari tempat pemberhentian semula.
Contoh soal keempat
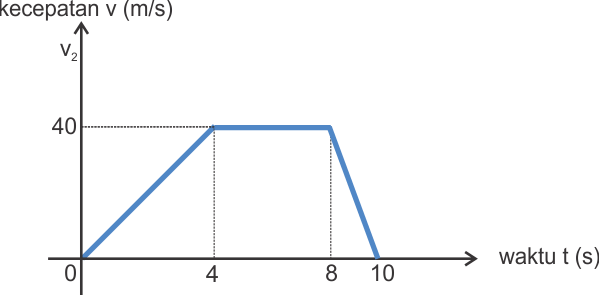
Sebuah benda bergerak sesuai dengan gambaran grafik di bawah ini yaitu sebuah grafik yang menghubungkan antara kecepatan (v) terhadap waktu (t).

a. Jelaskan gerakan partikel tersebut selama bergerak 10 detik?
b. Berapa jarak yang ditempuh benda tersebut selama 10 detik?
b. Berapa jarak yang ditempuh benda tersebut selama 10 detik?
Jawab
a. Pada waktu 4 detik pertama benda tersebut bergerak GLBB dengan nilai percepatan 10 m/s2. Kemudian bergerak GLB dengan kecepatan konstan sebesar 40 m/s selama 4 detik. Kemudian mengalami perlambatan sebesar -20 m/s2.
b. Untuk menghitung jarak total selama 10 detik, maka kita harus menjumlahkan jarak pada 4 detik pertama + jarak pada 4 detik kedua + jarak pada 2 detik terakhir.
b. Untuk menghitung jarak total selama 10 detik, maka kita harus menjumlahkan jarak pada 4 detik pertama + jarak pada 4 detik kedua + jarak pada 2 detik terakhir.
Dengan begitu, maka jarak (x) dapat kita ketahui dari persamaan (3) menjadi

atau menggunakan persamaan (2) menjadi
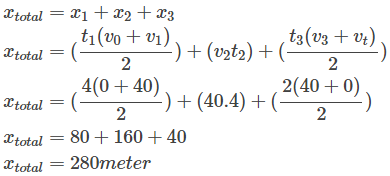
Jadi jarak total yang ditempuh benda tersebut sejauh 280 meter.
VIDEO PEMBELAJARAN GERAK LURUS BERATURAN (GLBB)
LATIHAN SOAL
Isilah google forms di bawah ini untuk mengerjakan latihan soal!
https://forms.gle/EWNDcLU4JQvNXyBJ7
Referensi:










